Materialien zum Unterricht
Darstellung von Zahlen
Zahlen sind für die Menschen seit Tausenden von Jahren ein wichtiges Mittel, um die Umwelt zu beschreiben und zu untersuchen. Die schriftliche Darstellung von Zahlen war der Ausgangspunkt für die Entwicklung von Schriften. In der Geschichte der Menschheit wurden viele unterschiedliche Zahlensysteme entwickelt, die in Konkurrenz zueinander standen.
Unser Dezimalsystem
Die Menschen haben nicht von Anfang an die Zahlen als Folgen der dezimalen Ziffern (0,1,2,3,4,5,6,7,8,9) dargestellt. Zuerst zählte man vermutlich mit den Fingern.
Wenn man alleine zählen möchte kommt man von 0 bis 10. Dann sind die Finger alle.
Wie könnte man weiter zählen?
Merke
Beispiel:
Kartendarstellung einer Dezimalszahl
Zahlen im Dezimalssystem können durch Karten mit den Werten 1, 10, 100, 1000, ... dargestellt werden.
Zehn Einerkarten haben den Wert einer Zehnerkarte.
Es gilt: 1⋅10= 10 , 10⋅10=100 , ...
Dadurch werden nie mehr als 9 Karten der gleichen Sorte benötigt.
Beispiel:
Die Zahl 6314 durch 6 Tausenderkarten, 3 Hunderterkarten, 1 Zehnerkarte und 4 Einerkarten dargestellt:
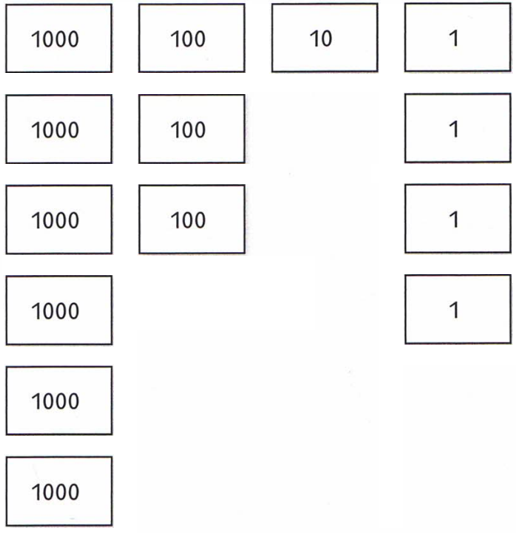
Es gilt dabei folgende Regel:
Die richtige Kartendarstellung ist diejenige, welche die kleinstmögliche Anzahl Karten benötigt (maximal neun Karten der gleichen Sorte).
Das Oktalsystem
Wie würde unser Zahlensystem aussehen wenn wir statt 10 nur 8 Finger gehabt hätten?
Die Micky Mouse und alle anderen Comicfiguren bekommen von ihren Zeichnern immer nur vier Finger pro Hand, haben also 8 Finger.
Wie zählt man eigentlich mit 8 Fingern?
Sie hat nur 8 Finger und kann deshalb alleine nur bis zur 7 zählen:
0, 1, 2, 3, 4, 5, 6, 7
Eine 8 und eine 9 gibt es in dieser Welt nicht, weil dafür zu wenig Finger da sind.
Wie zählen nun die Mäuse?
Nehmen wir an, auf dem Tisch liegen eine bestimmte Anzahl Äpfel.

Bis zum 7. Apfel wird in beiden Zahlensystem gleich gezählt.
Aber beim nächsten Apfel trennen sich die Wege: der Mensch kann mit seinen Fingern locker weiterzählen, die Micky Mouse jedoch ist am Ende angekommen.
Sie braucht jetzt einen Partner mit weiteren Fingern und zählt logisch weiter:
Die Anzahl der Äpfel auf dem Tisch ist für beide gleich.
Beim Zählen erhält der Mensch aber 12 Äpfel und die Micky Mouse 14 Äpfel.
Der Mensch zählt im Dezimalsystem und die Micky Mouse im Oktalsystem. (Oktal = 8)
Man kann schreiben:
12 dezimal = 14 oktal
Das Binärsystem
Angenommen ein Wesen hat nur einen einzigen Finger.
Das Wesen gehört zur Gattung der Binären.
Wie zählen die Binären?
Für sie gibt es nur zwei Ziffern: 0, 1
Der möchte auch die Äpfel zählen.

Er kann mit seinem nur einen Apfel zählen. Dann braucht er schon Hilfe.
Zu kommen sie bis zum 3. Apfel, müssen dann aber anfordern.
Nur zu schaffen sie es, alle Äpfel abzuzählen und
erhalten für den letzten den Wert 1100.
(Spricht: Eins, Eins, Null, Null)
Man kann schreiben:
12 dezimal = 14 oktal = 1100 binär
Computer
Alle Computer kommen aus der Welt der Binären. Sie haben nur einen Finger, oder besser gesagt, Schalter zum Zählen.
Ein Schalter kann nur zwei Zustände einnehmen:
oder .
Für den Zustand
sagen wir Null und für den Zustand
Eins.
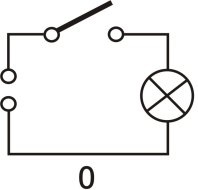
In der Computersprache wird eine Information, die eine Null oder eine Eins darstellen kann, als Bit bezeichnet.
Wieviel Bits sind notwendig, um eine Ziffer zwischen 0 und 9 darzustellen?
Dazu schauen wir uns noch mal das Apfelzählbild an:

Mit einem Bit kann man bis 1 zählen, mit 2 Bits schon bis 3.
Nimmt man ein weiters Bit dazu, kommt man bis 7.
Die Comicfiguren können sich bequem zurücklehnen.
Sie brauchen 3 Bits, um ihr Zahlensystem darzustellen.
Wir aber haben 10 Finger und brauchen ein weiters Bit.
Für das Dezimalzystem sind also 4 Bit notwendig.
Die Zuordnung sieht so aus:
Anscheinend haben wir Möglichkeiten unserer 4 Bit noch nicht ganz ausgeschöpft.
Mit 4 Bit lassen sich noch viel mehr Kombinationen darstellen.
Wie viele Zeilen könnte unsere Tabelle haben?
Mit 2 Bit lassen sich 4 Ziffern erzeugen, 0, 1, 2 und 3.
Man kann die vorhandenen Kombinationen mit einer 0 im neuen Bit und mit einer 1 im neuen Bit darstellen, die vorhandenen Zeilen also zweimal schreiben.
Da die Ziffern nach der 9 keine Bezeichnungen haben, hat man sich für große Buchstaben entschieden.
Die Ziffern und Buchstaben ergeben das Hexadezimalsystem.
Die vollständige Tabelle sieht nun so aus:
| Bit 3 | Bit 2 | Bit 1 | Bit 0 | Hexadezimal | Dezimalsystem |
|---|---|---|---|---|---|
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
1
|
1
|
1
|
|
0
|
0
|
1
|
0
|
2
|
2
|
|
0
|
0
|
1
|
1
|
3
|
3
|
|
0
|
1
|
0
|
0
|
4
|
4
|
|
0
|
1
|
0
|
1
|
5
|
5
|
|
0
|
1
|
1
|
0
|
6
|
6
|
|
0
|
1
|
1
|
1
|
7
|
7
|
|
1
|
0
|
0
|
0
|
8
|
8
|
|
1
|
0
|
0
|
1
|
9
|
9
|
|
1
|
0
|
1
|
0
|
A
|
10
|
|
1
|
0
|
1
|
1
|
B
|
11
|
|
1
|
1
|
0
|
0
|
C
|
12
|
|
1
|
1
|
0
|
1
|
D
|
13
|
|
1
|
1
|
1
|
0
|
E
|
14
|
|
1
|
1
|
1
|
1
|
F
|
15
|
In den rot markierten Zeilen ist immer nur ein Bit auf 1 gesetzt und kennzeichnet die Wertigkeit dieses Bits:
| Bit | Wert |
|---|---|
|
0
|
1
|
|
1
|
2
|
|
2
|
4
|
|
3
|
8
|
Rechnet man in der jeweiligen Zeile die Wertigkeiten der gesetzen Bits zusammen, erhält man den dezimalen Wert.
Da das in der Tabelle dargestellte Zahlensystem insgesamt 16 Ziffern beinhaltet, heißt es hexadezimales Zahlensystem.
Nice to know
Die ersten Mikrocontroller in den 70iger Jahren hatten ein Breite von 4 Bit und konnten eine Ziffer verarbeiten. Die Entwicklung ging schnell weiter und 8 Bit Breite wurde zum Standart.
Da in der Mikroelektronik ständig die vorhandene Bitzahl verdoppelt wird, war nach den 8 Bit der nächste Schritt 16 Bit und dann 32 Bit. Zur Zeit arbeiten wir mit 64 Bit.
Es gilt: 8 Bit = 1 Byte
Mit 8 Bit lassen sich insgesamt 256 Möglichkeiten darstellen und das reicht aus, um neben Ziffern auch Buchstaben zu übertragen.





