1) Geordnete Stichprobe mit Zurücklegen  n^k

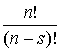
1. a) In einen Urne liegen 10 Kugeln mit den Nummern 1 bis 10. Man zieht eine Kugel zufällig, notiert ihre Nummer und legt sie dann wieder zurück. Wie viele verschiedene Zahlenfolgen erhält man, wenn man 6-mal zieht?
b) In einen Urne liegen n Kugeln mit den Nummern 1 bis n. Man zieht eine Kugel zufällig, notiert ihre Nummer und legt sie dann wieder zurück. Wie viele verschiedene Zahlenfolgen erhält man, wenn man s-mal zieht?

2. Es gibt eine andere Version obiger Aufgabe, die für manche Anwendungen bequemer ist. Statt 6 Kugeln aus einer Urne zu ziehen, legen wir 6 unterscheidbare Kugeln in 10 unterscheidbare Urnen. Die Kugeln sollen irgendwie auf die Urnen verteilt werden. Jede Urne darf beliebig viele Kugeln enthalten. Berechne die Anzahl der Möglichkeiten.

3. Berechne die Anzahl der verschiedenen Würfe, die man mit 3 (unterscheidbaren ) Würfeln erzielen kann

4. Ein Autofahrer muss auf seiner Fahrt 4 Ampeln passieren. Jede Ampel hat 3 Phasen: grün, orange, rot. Die Ampeln sind nicht aufeinander abgestimmt. Berechne die Anzahl der Möglichkeiten.

5. Aus weißen und roten gleich großen Legosteinen werden aus 4 Steinen „ Türme“ zusammengesetzt. Berechne die Anzahl der möglichen verschiedenen „Türme“

6. Bei einem Kombinationsschloss sind die einzelnen Einstellungen durch 3-ziffrige Zahlen mit Ziffern aus 1 bis 9 möglich. Berechne die Anzahl der möglichen Einstellungen.

7. Berechne auf wie viele Arten eine Kolonne eines Fußball-Totoscheines (1,2,x) für 12 Spiele ausgefüllt werden kann.

1. a) In einer Urne liegen 10 Kugeln mit den Nummern 1 bis 10.
Man zieht nacheinander 6 Kugeln ohne Zurücklegen und notiert ihre Nummern in der Reihenfolge, in der sie erscheinen. Wie viele Möglichkeiten gibt es?
b) In einer Urne liegen n Kugeln mit den Nummern 1 bis n.
Man zieht nacheinander s Kugeln ohne Zurücklegen und notiert ihre Nummern in der Reihenfolge, in der sie erscheinen. Wie viele Möglichkeiten gibt es?
c) In einer Urne liegen n mit den Nummern 1 bis n.
Man zieht nacheinander alle Kugeln ohne Zurücklegen und notiert ihre Nummern in der Reihenfolge, in der sie erscheinen. Wie viele Möglichkeiten gibt es?

2. Eine Fußballmannschaft besteht bekanntlich aus 11 Spielern Der Trainer entscheidet sich dafür, 5 Spieler der Mannschaft für das Elfmeterschießen auszuwählen und gleichzeitig die Reihenfolge festzulegen, in welcher die 5 Spieler zum Elfmeter antreten sollen. Wie viele Möglichkeiten gibt es für dieses Auswahlverfahren? 

3. 16 Personen wollen mit einem Autobus fahren, der genau 5 freie Plätze hat. Wie viele Möglichkeiten gibt es die 5 Plätze zu besetzen, wenn die verschiedenen Anordnungen der Personen berücksichtigt werden? 

4. Möglichkeiten der Belegung der ersten drei Plätze bei einem Pferderennen, an dem 5 Pferde teilnehmen? 

5. Es sollen 5 unterscheidbare Kugeln auf 9 unterscheidbare Urnen verteilt werden. In einer Urne darf höchstens eine Kugel liegen. Wie viele Verteilungen gibt es?

6. Für ein Projekt soll aus 7 Bewerbern ein Projektleiter und ein Stellvertreter bestimmt werden.

7. Bei einer Wahl bewerben sich 4 Kandidaten für den Posten des Bürgermeisters. Möglichkeiten des Wahlausgangs, wenn der Kandidat, der am zweithäufigsten gewählt wurde. Vizebürgermeister wird.

8. Bei „Dreiereinlaufwetten“ starten 8 Pferde, die Belegung der ersten drei Plätze ist von Bedeutung. Wie viele Möglichkeiten gibt es hierfür?

9. Wie viele Möglichkeiten gibt es, um aus den 39 Mitgliedern eines Vereins einen Präsidenten und einen Vizepräsidenten auszuwählen

1. a) In einer Urne sind 10 Kugeln mit den Nummern 1 bis 10. Es werden mit einem Griff 6 Kugeln gezogen (Die Reihenfolge zählt daher nicht). Wie viele Möglichkeiten gibt es?
b) Aus n unterscheidbaren Kugeln sollen s Kugeln mit einem Griff gezogen werden. Wie viele Möglichkeiten gibt es?

2. Eine Fußballmannschaft besteht bekanntlich aus 11 Spielern Der Trainer will für Elfmeterschießen 5 Spieler aus seiner Mannschaft auswählen. Wie viele Möglichkeiten hierfür gibt es?

3. 16 Personen wollen mit einem Autobus fahren, der genau 5 freie Plätze hat. Wie viele Möglichkeiten gibt es die 5 Plätze zu besetzen, wenn die verschiedenen Anordnungen der Personen nicht berücksichtigt werden?

4. Aus einer Menge von 20 Pferden sollen 8 Pferde ausgewählt werden, die an einem Rennen teilnehmen.

5. In einer Klausur müssen zwei von vier zur Wahl gestellten Aufgaben bearbeitet werden. Wie viele verschiedene Kombinationen sind möglich?

6. Zwei von 29 Schülern einer Klasse werden für den Tafeldienst ausgewählt. Wie viele verschiedene Kombinationen sind möglich?

7. Aus 7 Bewerbern sind zwei Personen auszuwählen, die an einem Projekt mitarbeiten

8. Aus 10 Kandidaten sollen 4 Personen gewählt werden, die einen Sitz in einem bestimmten politischen Ausschuss erhalten.

a) Berechne die Anzahl der Möglichkeiten, die eine Organisation mit 30 Mitgliedern hat, um einen Vorsitzenden, einen Stellvertreter, einen Schriftführer und einen Kassier zu wählen, wenn Ämterkumulierung ausgeschlossen wird! 
b) Dieselbe Organisation wählt 2 Rechnungsprüfer. Berechne die Anzahl der Wahlmöglichkeiten, wenn jedes der übrigen 26 Mitglieder bereit ist, im falle der Wahl diese Funktion anzunehmen!

9. Beim Süddeutschen Lotto sind aus 49 Zahlen 6 auszuwählen. Wie viele Möglichkeiten gibt es hierfür?

10 Wie viele Möglichkeiten gibt es, um aus einer Menge von 13 Fußballspielern 11 Spieler auszuwählen?

11. Aus 5 Ehepaaren werden 4 Personen ausgewählt. Die ausgewählten Personen sollen 2 Männer und 2 Frauen sein

12. Zehn Personen verabschieden sich nach einer Feier per Handschlag.
a) Wie oft werden die Hände geschüttelt?
b) Wie oft werden die Hände geschüttelt, wenn es sich bei den 10 Personen um 5 Ehepaare handelt?

Verschiedene Aufgaben

1.    Eine Fußballmannschaft besteht bekanntlich aus 11 Spielern
Die 11 Spieler verlassen vor Spielbeginn der Reihe nach die Mannschaftskabine. 
Wie viele verschiedene Reihenfolgen sind dabei möglich?
 

2.    Der Trainer will für ein Elfmeterschießen 5 Spieler aus seiner Mannschaft auswählen. 
Wie viele Möglichkeiten hierfür gibt es?

 

3.    Der Trainer entscheidet sich dafür, 5 Spieler der Mannschaft für das Elfmeterschießen auszuwählen und gleichzeitig die Reihenfolge festzulegen, in welcher die 5 Spieler zum Elfmeter antreten sollen. 
Wie viele Möglichkeiten gibt es für dieses Auswahlverfahren?

 

4.   Bei einer Stadteinfahrt hat man 6 Ampeln zu passieren. Bei jeder Ampel hat man die zwei Möglichkeiten: „Anhalten“ - „Fahren“. 
Auf wie viele verschiedene Arten kann man die 6 Ampeln passieren? 

 

5.    Jemand besitzt 7 CD´s mit klassischer Musik, 12 CD´s mit Popmusik und 5 CD´s mit Jazz. Wie können die 25 CD´s in einer Reihe angeordnet werden, wenn sie gruppenweise beieinanderstehen sollen?  

 

6.    Bei einem Fahrradschloss können auf drei Ringen jeweils die Ziffern 1 bis 6 eingestellt werden. 
a) Wie viele verschiedene Möglichkeiten hat man, eine Zahlenkombination einzustellen?
b) Ein Dieb weiß, dass der Fahrradbesitzer eine Vorliebe für gerade Zahlen hat. Er möchte alle Zahlenkombinationen probieren, die an der ersten und an der letzten Stelle eine gerade Ziffer haben. Wie viele derartige Kombinationen gibt es?

 

7.    Auf wie viele Arten kann man aus der 8a, der 8b und der 8c Klasse ein Maturaballkomittee bilden, wenn es aus 2 Schülern jeder Klasse gebildet wird? (8a...26 Schüler, 8b...23 Schüler und 8c... 18 Schüler) 

 

8.    Auf wie viele Arten kann man bei der Wienwoche mit 20 Schülern ein 4- und zwei 8-Bettzimmer belegen?

 

9.    Auf wie viele Arten kann man 20 verschiedene Ostereier auf drei verschiedenartige Nester verteilen?

 

10. Bei einem Fest stoßen alle sechs der Anwesenden miteinander an, nacheinander und jeder mit jedem einmal. 
Wie oft erklingen die Gläser? 

 

11. Auf wie viele Arten können 20 Schüler in einem Klassenzimmer Platz nehmen,
a) wenn kein Platz frei bleibt?
b) wenn vier von 24 Plätzen frei bleiben? 

 

12. Auf wie viele Arten kann man 30 verschiedene Ostereier auf drei verschiedenartige Nester verteilen, so dass in jedem Nest gleich viele liegen? 

 

13. Bei einem Fest sind sechs Ehepaare anwesend. Nach einem speziellen Trinkspruch stoßen alle Männer mit allen Frauen an (nicht gleichgeschlechtlich). Wie oft erklingen die Gläser?

 

14. Ein Computerhändler verkauft seine sonst gleichartigen Computer mit fünf verschiedenen Monitoren, drei verschiedenen Festplatten und zwei verschiedenen Größen des Arbeitsspeichers. Er hat alle möglichen Konfigurationen aufgebaut in seinem Laden stehen. Wie viele Computer müssen mindestens im Laden stehen? 

 

15. Bei einem Pferderennen kommen die Pferde mit den Startnummern 6, 19, 25, 27 ins Stechen (Zieleinlauf). Wie viele verschiedene Wetten können auf den 1. und 2. Platz (gemeinsam) abgeschlossen werden? 

 

16. Jemand kann mit vier verschiedenen Fluglinien zwischen Wien und Paris fliegen. Wie viele Möglichkeiten hat er, eine Fluglinie für einen Flug von Wien nach Paris und zurück auszuwählen, wenn
a) er für beide Flüge dieselbe Fluglinie
b) er nicht unbedingt für beide Flüge dieselbe Fluglinie
c) er für beide Flüge auf jedem Fall verschiedene Fluglinien wählt

 

17. Eine Lieferung von 50 Transistoren enthält 40 intakte und 10 defekte Stücke. Auf wie viel Arten kann man genau 3 intakte und 2 defekte Transistoren auswählen?

 

18. An einer Rechenanlage können Variable mit maximal 5 Zeichen gebildet werden, wobei das erste Zeichen nur eines der 26 Buchstaben sein darf, die folgenden hingegen Buchstaben oder Ziffern (Zeichenwiederholung ist erlaubt)
a) Wie viele Variablennamen mit genau 5 Zeichen können gebildet werden?
b) Wie viele Möglichkeiten bestehen insgesamt Variablennamen zu bilden?
c) wie würden sich die Variablenanzahl in Frage a) ändern, wenn eine Zeichenwiederholung nicht erlaubt ist?